Simpangan rata-rata, juga dikenal sebagai deviasi rata-rata atau mean deviation, adalah ukuran statistik yang menggambarkan seberapa jauh nilai-nilai dalam suatu kumpulan data menyimpang dari nilai rata-ratanya. Konsep ini memberikan gambaran tentang variabilitas atau penyebaran data dalam suatu distribusi.
Salah satu kegunaan simpangan bagi statistika adalah membantu memahami pengukuran data.
Simpangan tidak hanya dapat digunakan dalam penelitian saja, melainkan bisa diterapkan dalam proses manajemen perusahaan.
Karena itulah, simpangan bisa dijadikan landasan dalam proses pengambilan keputusan dan perencanaan manajemen.
Kegunaan simpangan rata rata
- Membantu memahami pengukuran data
- Memudahkan proses perhitungan dan pengukuran nilai data atau angka
- Mengukur variabilitas nilai rata-rata
- Menunjukkan besaran nilai yang tersebar dalam suatu data
- Menguji hipotesis
- Membantu proses pengambilan keputusan dan perencanaan manajemen.
Cara Untuk Mencari Nilai Simpangan
Ada beberapa cara dan juga tahapan yang harus dilakukan untuk bisa menentukan nilai simpangan baku. Maka dari itu, ikutilah langkah-langkah berikut ini sebagai runutan dari proses mencari nilai simpangan dalam sebuah data.
1. Menghitung Nilai Rata-Rata
Nilai rata-rata atau mean dapat dihitung dengan menjumlahkan keseluruhan data yang ada dan dibagi dengan jumlah data tersebut. Nilai rata-rata sama dengan jumlah dari setiap nilai yang ada di dalam sebuah kumpulan data. Selanjutnya dibagi dari total data.
2. Hitung Penyimpangan Titik Data
Caranya adalah dengan mengurangi nilai dari rata-rata data dengan setiap titik data yang ada. Selanjutnya masih ada beberapa tahapan lagi yang harus dilakukan untuk bisa mendapatkan nilai dari simpangan yang berbentuk baku.
3. Mencari Nilai Varian
Caranya adalah dengan mengkuadratkan simpangan dari setiap titik data dan mencari penyimpangan kuadrat individu dari nilai rata-ratanya. Inilah yang disebut dengan nilai varian. Langkah ini cukup mudah dilakukan, tetapi mungkin memerlukan alat bantu hitung apabila angkanya tidak bulat.
4. Mencari Akar Kuadrat dari Nilai Varian
Tahap terakhir adalah mencari akar kuadrat dari nilai varian yang sudah didapatkan. Ini adalah merupakan hasil dari simpangan yang berbentuk baku. Kamu sudah bisa mendapatkan hasilnya dan melihatnya apakah lebih besar, lebih kecil, atau bahkan sama dengan nol.
Rumus Simpangan Rata-rata
Secara garis besar, rumus simpangan rata-rata dibagi menjadi dua, yakni simpangan rata-rata data tunggal dan simpangan rata-rata berkelompok.
1. Rumus Simpangan rata-rata tunggal

Keterangan:
SR: simpangan rata-rata
X: data ke-i, ada juga yang menyimbolkan dengan xi
X dengan akses garis di atas: nilai rata-rata data
n: banyak data
2. Rumus Simpangan rata-rata kelompok
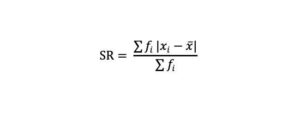
Keterangan:
SR: simpanan rata-rata
Xi: data ke-i
x aksen: nilai rata-data data
fi atau f: total frekuensi
Contoh soal
1. Soal: Hitunglah simpangan rata-rata dari data berikut: 5, 7, 8, 10, 12
Pembahasan:
Hitung rata-rata: (5 + 7 + 8 + 10 + 12) / 5 = 42 / 5 = 8.4
Hitung selisih setiap data dengan rata-rata: |5 – 8.4| = 3.4 |7 – 8.4| = 1.4 |8 – 8.4| = 0.4 |10 – 8.4| = 1.6 |12 – 8.4| = 3.6
Jumlahkan semua nilai mutlak: 3.4 + 1.4 + 0.4 + 1.6 + 3.6 = 10.4
Bagi hasil penjumlahan dengan jumlah data: 10.4 / 5 = 2.08
Jadi, simpangan rata-rata dari data tersebut adalah 2.08.
2. Coba hitung simpangan rata-rata dari data dibawah ini:
| Interval Nilai | Frekuensi |
| 1-3 | 3 |
| 4-6 | 4 |
| 7-9 | 5 |
| 10-12 | 8 |
| 13-15 | 5 |
Langkah pertama, kamu perlu mencari tahu dulu nilai tengah (xi).
| Intervensi Nilai | Frekuensi (fi) | Nilai tengah (xi) | Fi.xi |
| 1-3 | 3 | 2 | 6 |
| 4-6 | 4 | 5 | 20 |
| 7-9 | 5 | 8 | 40 |
| 10-12 | 8 | 11 | 88 |
| 13-15 | 5 | 14 | 70 |
| Total | 25 | 224 |
Setelah itu mencari x aksen dengan menggunakan rumus dibawah ini:
x aksen =
x aksen =
x aksen = 8,96
Kemudian kamu perlu mencari simpangan rata-rata dari masing-masing interval data untuk menentukan ∑ fi,xi aksen pada rumus. Caranya adalah:
| Interval nilai | (fi) | (xi) | Fi.xi | |xi-x aksen| | Fi|xi-x aksen| |
| 1-3 | 3 | 2 | 6 | |2-8,96| = 6,96 | 20,88 |
| 4-6 | 4 | 5 | 20 | |5-8,96| = 3,96 | 15,84 |
| 7-9 | 5 | 8 | 40 | |8-8,96| = 0,96 | 4,8 |
| 10-12 | 8 | 11 | 88 | |11-8,96| = 2,04 | 16,32 |
| 13-15 | 5 | 14 | 70 | |14-8,96| = 5,04 | 25,2 |
| Total | 25 | 224 | 83,04 |
Langkah terakhir, kamu masukkan hasilnya ke rumus awal untuk mencari simpangan rata-rata.
SR = 83,4 : 25 = 3,336